Calculating the Hardy-Weinberg ratio

Let us work out the Hardy-Weinberg ratio for the genotype AA.

AA individuals come from matings AA x AA, AA x Aa (and Aa x AA) , and Aa x Aa matings. We can ignore all the other types of mating.

AA x AA matings have frequency P² andproduce all AA offspring, AA x Aa and Aa x AA matings each have frequency PQ and produce 1/2 AA offspring.

Aa x Aa matings have frequency Q² and produce 1/4 AA offspring. The frequency of AA in the next generation, P', is then: P' = P² + (1/2)PQ + (1/2)PQ + (1/4)Q² This can be rearranged to

P' = (P + (1/2)Q ) ( P + (1/2)Q ).

(P + 1/2Q ) , we have seen, is simply the frequency of the gene A, referred to as p. Therefore

P' = p²

The frequency of genotype AA after one generation of random mating is equal to the square of the frequency of the A gene. Analogous arguments show that the Hardy-Weinberg frequencies are then:

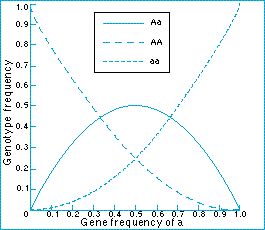
Genotype AA : Aa : aaFrequency p² : 2pq : q²

The Hardy-Weinberg genotype frequencies are reached after a single generation of random mating from any initial genotype frequencies. Imagine, for example, two populations with the same gene frequency but different genotype frequencies. One population has 750 AA , 0 Aa , 250 aa ; the other has 500 AA , 500 Aa , 0 aa . p = 0.75, q = 0.25 in both. After one generation of random mating, the genotype frequencies in both will become 558 AA, 375 Aa , 67 aa if the population size remains 1000. (Fractions of an individual have been rounded to make the numbers add to 1000. The proportions are 9/16, 6/16, 1/16.) After reaching those frequencies immediately, in one generation, the population stays at Hardy-Weinberg equilibrium for as long as the population size is large, there is no selection, and mating is random.

Figure: Hardy-Weinberg proportions of genotypes AA, Aa and aa in relation to the frequency of the gene a.