The units of selection - Does a gene ever benefit at the expense of an allele?
Explaining why meiotic drive is rare
If segregation distortion genes have such a great selective advantage, why aren't they more widespread?
• Recombination breaks down the segregation distortion gene complex
Any system for distorting meiotic segregation is theoretically likely to require at least two linked genes (one for recognition, one for distortion). The genes have to be linked in order to spread: if recombination separated the effecter gene from the recognition sequence, it would be liable to work against itself.
Segregation distortion systems are particularly likely to be found in regions of the genome in which the recombination rate is low, or zero. Perhaps recombination itself evolved to break up co-operating sets of distorter genes.
• Segregation distortion is evolutionarily short-lived
We can imagine the following series of evolutionary events. At each locus, selection favors mutant alleles that can get into more than 50% of the offspring; whenever such an allele arises it has an automatic advantage.
Once it has arisen, the next stage will depend on the fertility of its bearer. If it has no effect on, or increases, fertility, its frequency should increase to one. If it reduces fertility, alleles at other loci that suppress the effect will be favored; in this case, the distorter gene will either be suppressed, or increase to a fixation, depending on how quickly a suppressor allele arises.
In either case, segregation distortion will be evolutionarily short-lived. The allele responsible will either be fixed (and segregation distortion then disappears) or suppressed. At any one time, only a few cases should exist. This probably explains why only a few have been found. Meiosis generally does appear to be fair; alleles usually are equally represented in the offspring. It is important to remember, however, that this fairness exists despite selection at each locus for alleles that subvert the Mendelian ratios.
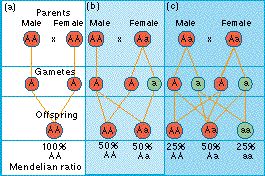
Figure: Mendelian ratios are almost universal in nature. (a) For an AA x AA cross. (b) For an AA x Aa cross. (c) For an Aa x Aa cross.
| Next |